[最も選択された] 円錐 中��角 求め方 比 305271-円錐 中心角 求め方 比
円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
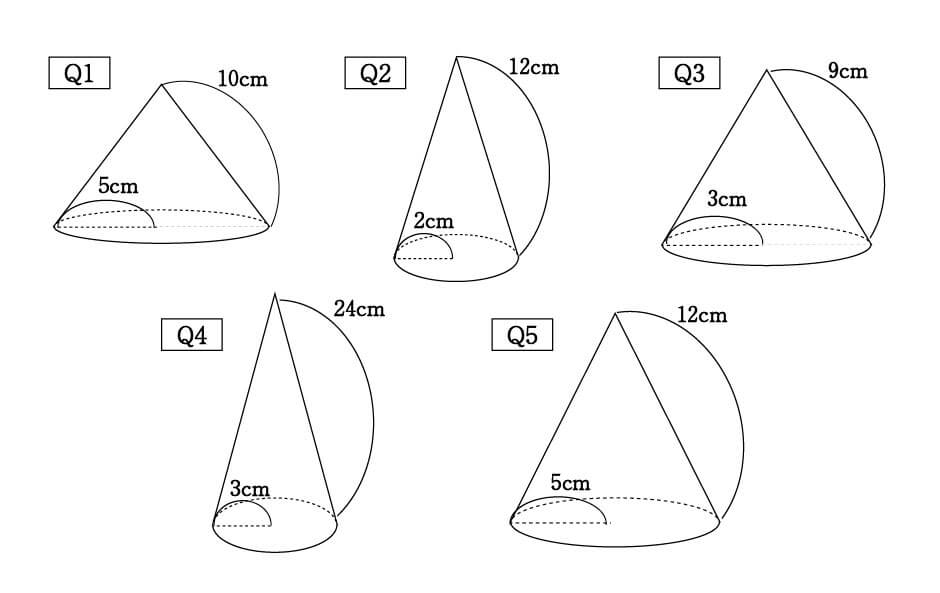
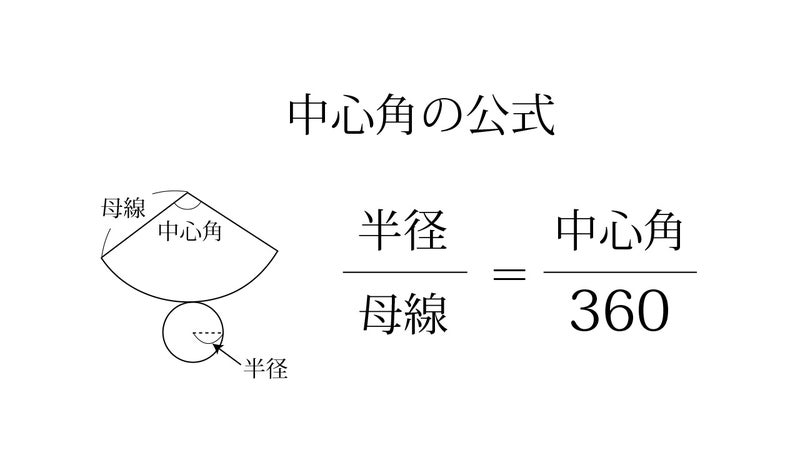
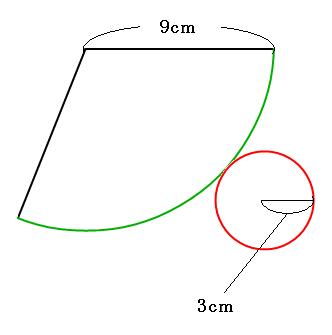
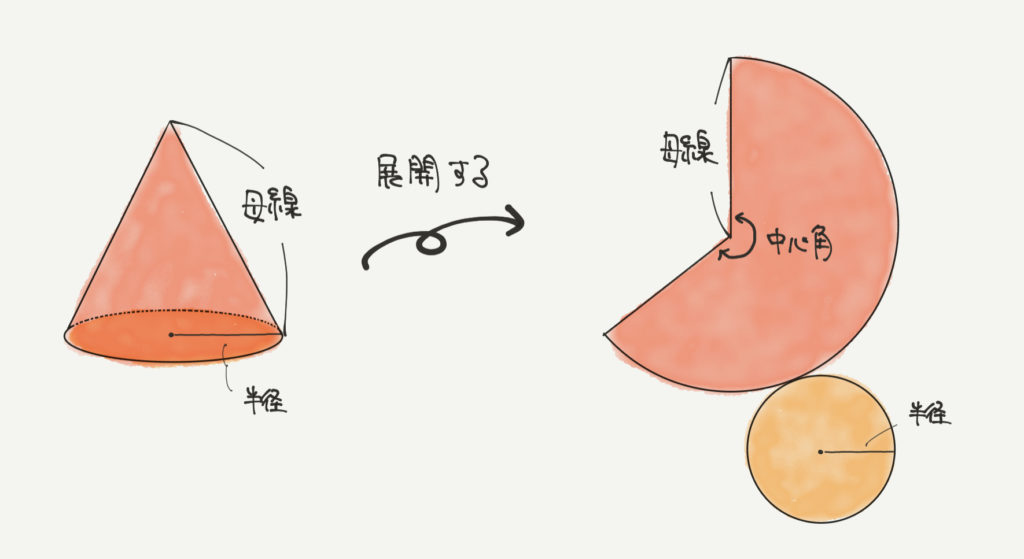
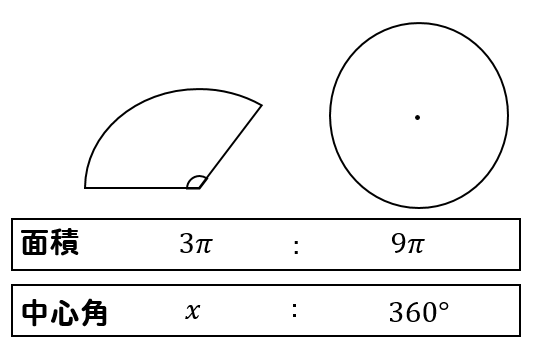
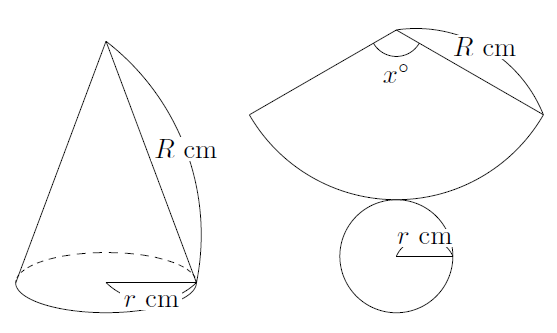
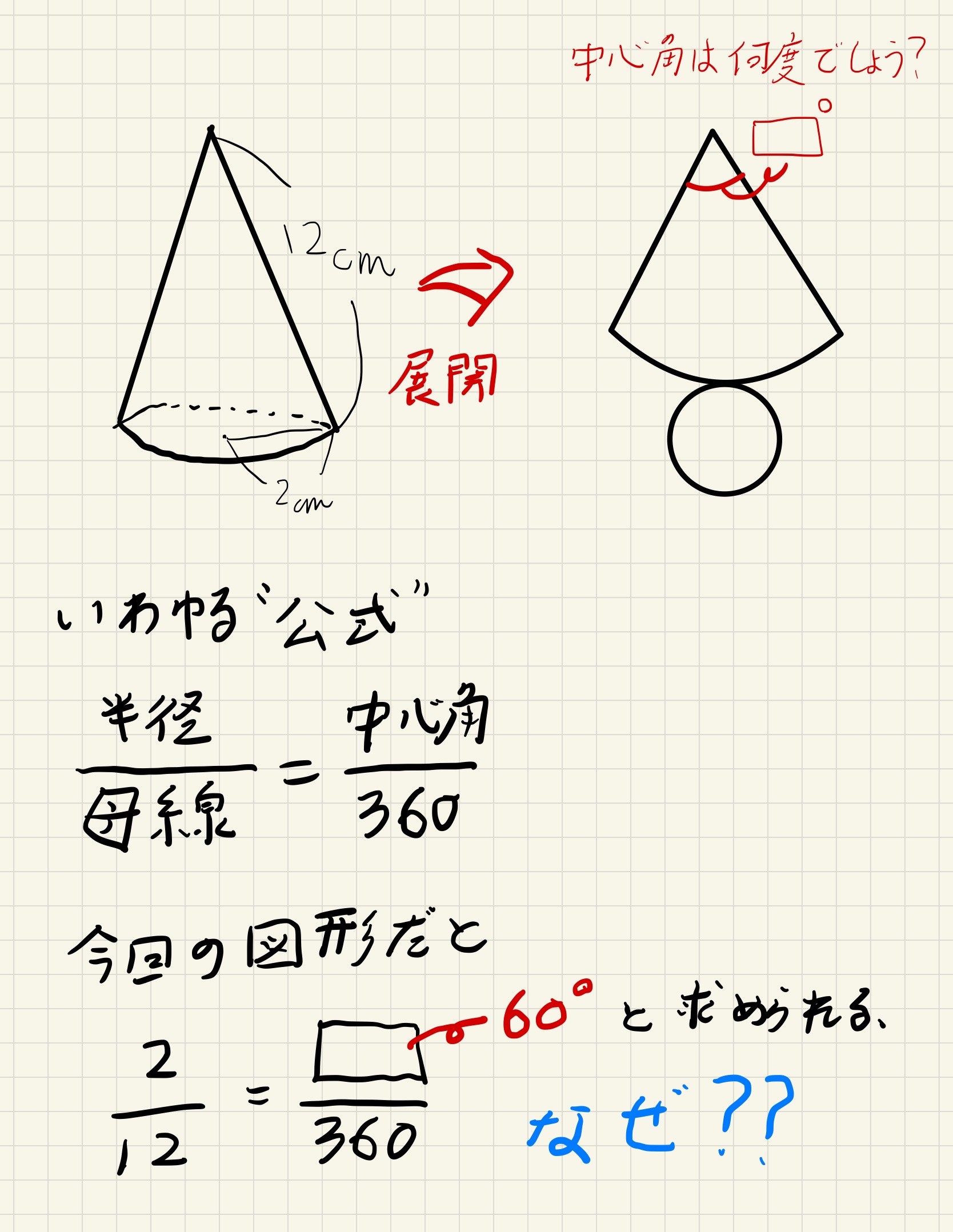
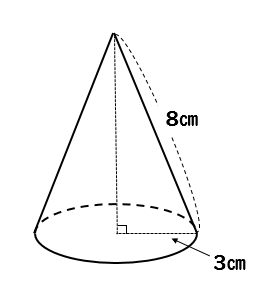
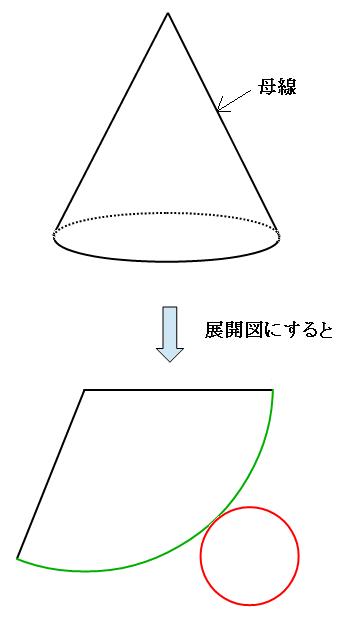
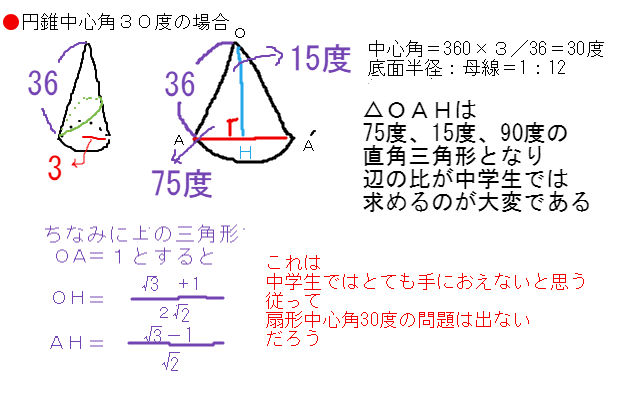
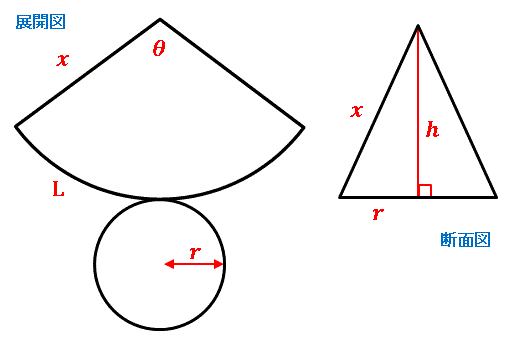
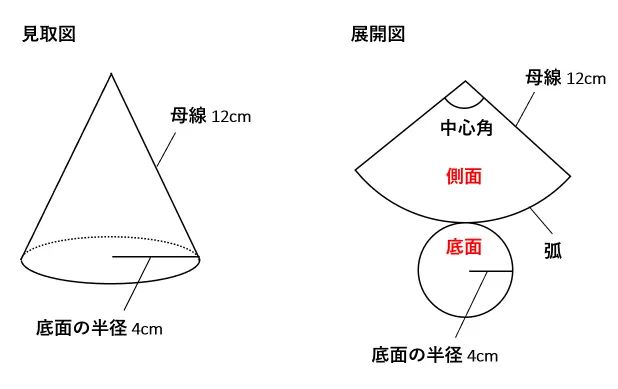
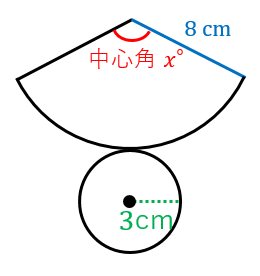
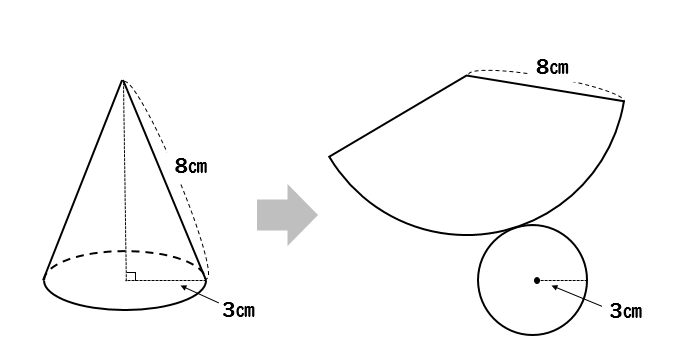
円錐の中心角を求める公式は次のとおり。 円錐の中心角の公式 ・ 円錐の中心角\ (\hskip2pt=\frac {r} {l}\times360^\circ\) なお ・ 円錐の中心角とは、円錐を展開してできるおうぎ形の中心角のこと として、ここではハナシを進めていきます。 それでは円錐の そこで今回は、円錐の側面の中心角を簡単に出す公式を紹介します。 円錐の側面積の中心角 = 360° × 低面の半径 ÷ 母線 下の図で側面の中心角を求めると、 上の図より、母線=9、円の半径=3なので、 円錐の側面の中心角 = 360° ×底面の半径 ÷ 母線 = 360° × 3 ÷ 6 = 1° となります。 にほんブログ村 目次 見る おすすめ教材 ここからは、中学生にお勧めの教材を紹介します。
円錐 中心角 求め方 比
円錐 中心角 求め方 比-展開図を描く段階では、おうぎ形の中心角が分からない状態なので、概形(だいたいの図)で問題ない。 さて円錐の表面積の求め方は少々長いが、理解していただけただろうか。 手順としては ということを行っている。 このうち3については 前章・弧立体角の計算例 円錐の立体角は、 2 π ( 1 − cos θ 0) という公式で計算することができます。 ただし、 θ 0 は円錐の中心軸と母線がなす角度(平面角)です。 円錐の底面を円板をみなせば、「円板が張る立体角の公式」と言うこともできます。
数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
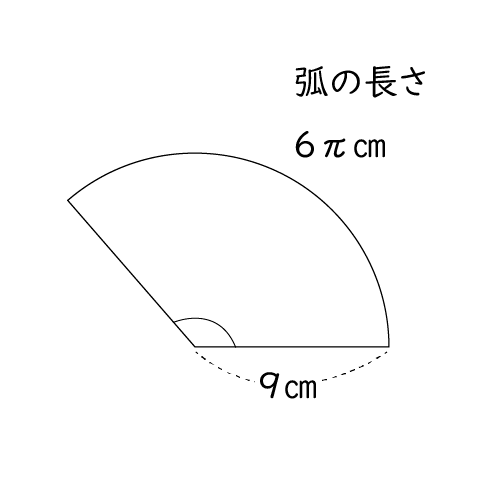
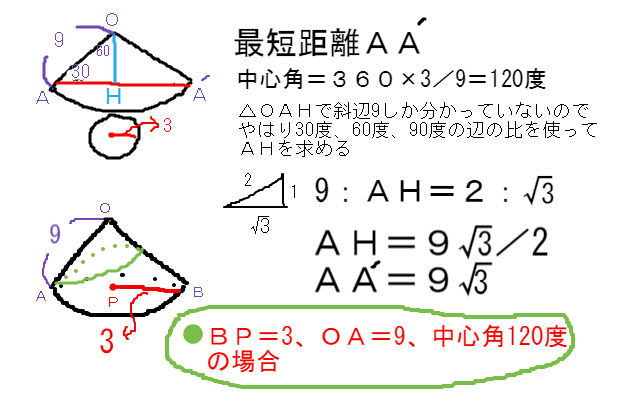
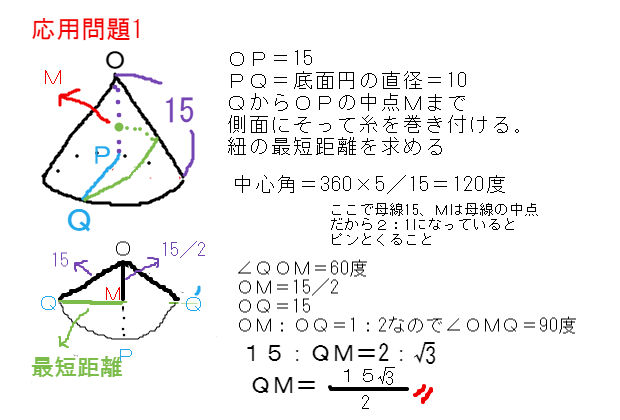
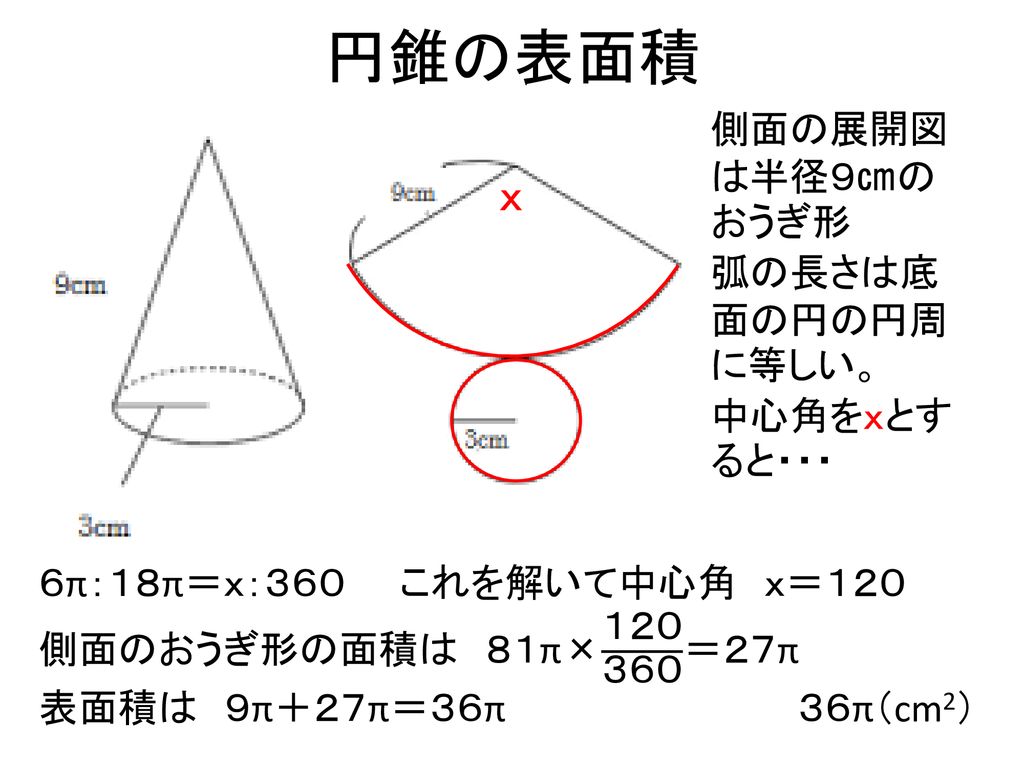
表面積 = 側面積 底面積 底面積は 9 π c m 2 、側面積は 15 π c m 2 よって、表面積は 15 π 9 π = 24 π c m 2 母線の長さ 問題図のような円錐を、Oを中心に転がすと、 3 回転してもとの位置に戻りました。 円錐の母線の長さを求めなさい。 3 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 3 枚分の長さ と等しくなります。 おうぎ形の弧の長さは、 2 × 6 × π = 12 π c 母線 × 中心角 / 360° = 半径 ↑両辺を「母線」で割ると・・・ 半径 / 母線 = 中心角 / 360° となるわけです! この考え方さえ理解していれば、たとえば中心角がわからないような問題でも 半径と母線 の長さがわかっていれば求めることができます。 この まとめ:円錐の母線の長さの求め方はだいたい2つしかない! この2つのパターン以外にも、 円錐の「半径」と「表面積」が与えられた場合 円錐の「底面の円周の長さ」と「側面の中心角」が与えられた場合 とかとか色々ある。 正直、ちょっと混乱し
円周角 とは、文字で表すと、 「円周上に点を3つ置き、3点を2本の線分でつないだ時、その2本の線で出来た角」 のことをいいます。 図形についてを言葉使って説明しても全然伝わらないと思うので、図を示して説明していきますね。 上のような円があっ 円錐の展開図で 底面積に当たる下部の半径は4cm 円錐部分(扇形)の半径は10cm その時の底面の周の長さは 直径 x π で8πと思うのですが回答は 2π x 4 の8πでした。 更に扇形の中心角は y = 360 x 4/10 で解けると思ったのですが回答は 2π x10x a/360=8π でした。 もちろん答えは同じものですが なぜ上記2問の問題集の式は 2π x 4 2π x10x a/360=8π だったのでしょうか? 2πはどこ これがわかれば、 中心角の大きさは、側面と底面の半径の比と同じになることが実感として理解できます 。 あとは式からでも押せますね。 中心角の角度は360°に対して「半径/母線」の割合になります。 よって側面を求める式は、 母線×母線×半径/母線
円錐 中心角 求め方 比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 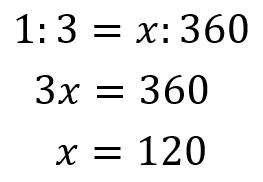 |  |
 | ||
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円錐 中心角 求め方 比」の画像ギャラリー、詳細は各画像をクリックしてください。
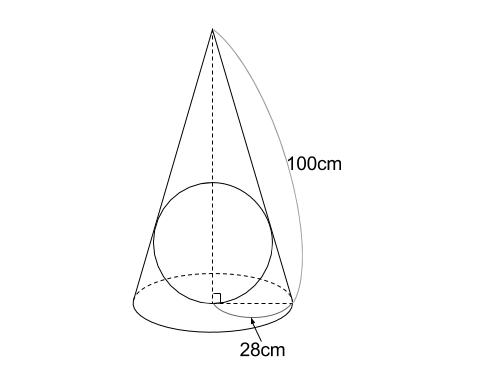
側面のおうぎ形の中心角の大きさ=底面の半径×360÷母線 側面の面積=底面の半径×母線×円周率 (例題2) 上の図は、底面の半径が9cmの円錐から、上の部分を切り取ったものです。 この図形の表面積は何cm²でしょう。 まずはこの図形の展開図を書いてみ 教えてください! 円錐は、母線の長さが分からなくても 中心角って求めることが出来るんですか? 求めれるならその求め方を教えてください< (_ _)> 底面の円の半径が5cmの円錐の体積と半径が5cmの球の体積が等しいとき、円錐の高さを求めなさい。 と
Incoming Term: 円錐 中心角 求め方 比,
コメント
コメントを投稿